Bezier Curves
How use?
Visualize and understand how Bezier curves can be programmed
Click button A[z] or B[x] to switch between Quadratic curve and Cubic curve
Code:
-- Initial x and y x, y = 120, 120
-- Set starter bezier mode = 1
-- Lerp function function lerp(x1, y1, x2, y2, t) local x = x1 + (x2-x1) * t local y = y1 + (y2-y1) * t return {x,y} end
-- Quadratic bezier function bezierQuad(x1,y1,x2,y2,x3,y3) -- Clay squares for i = 0,1.0001, 0.1 do local x = lerp(lerp(x1,y1,x2,y2,i)[1],lerp(x1,y1,x2,y2,i)[2],lerp(x2,y2,x3,y3,i)[1],lerp(x2,y2,x3,y3,i)[2],i)[1] local y = lerp(lerp(x1,y1,x2,y2,i)[1],lerp(x1,y1,x2,y2,i)[2],lerp(x2,y2,x3,y3,i)[1],lerp(x2,y2,x3,y3,i)[2],i)[2] line(lerp(x1,y1,x2,y2,i)[1],lerp(x1,y1,x2,y2,i)[2],lerp(x2,y2,x3,y3,i)[1],lerp(x2,y2,x3,y3,i)[2],15) end -- Lines of bezier local xlast = x1 local ylast = y1 for i = 0,1.01, 0.01 do local x = lerp(lerp(x1,y1,x2,y2,i)[1],lerp(x1,y1,x2,y2,i)[2],lerp(x2,y2,x3,y3,i)[1],lerp(x2,y2,x3,y3,i)[2],i)[1] local y = lerp(lerp(x1,y1,x2,y2,i)[1],lerp(x1,y1,x2,y2,i)[2],lerp(x2,y2,x3,y3,i)[1],lerp(x2,y2,x3,y3,i)[2],i)[2] line(xlast, ylast, x, y,2) xlast, ylast = x, y end end
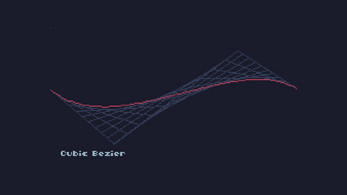
-- Cubic bezier function bezierCub(x1,y1,x2,y2,x3,y3,x4,y4) -- Clay squares for i = 0,1.0001, 0.1 do line(lerp(x1,y1,x2,y2,i)[1],lerp(x1,y1,x2,y2,i)[2],lerp(x2,y2,x3,y3,i)[1],lerp(x2,y2,x3,y3,i)[2],15) line(lerp(x2,y2,x3,y3,i)[1],lerp(x2,y2,x3,y3,i)[2],lerp(x3,y3,x4,y4,i)[1],lerp(x3,y3,x4,y4,i)[2],15) line(xb1, yb1, xb2, yb2, 15) --line(lerp(xb1,yb1,xb2,yb2,i)[1],lerp(xb1,yb1,xb2,yb2,i)[2],15) end -- Lines of bezier local xlast = x1 local ylast = y1 for i = 0,1.01, 0.01 do local xb1 = lerp(lerp(x1,y1,x2,y2,i)[1],lerp(x1,y1,x2,y2,i)[2],lerp(x2,y2,x3,y3,i)[1],lerp(x2,y2,x3,y3,i)[2],i)[1] local yb1 = lerp(lerp(x1,y1,x2,y2,i)[1],lerp(x1,y1,x2,y2,i)[2],lerp(x2,y2,x3,y3,i)[1],lerp(x2,y2,x3,y3,i)[2],i)[2] local xb2 = lerp(lerp(x2,y2,x3,y3,i)[1],lerp(x2,y2,x3,y3,i)[2],lerp(x3,y3,x4,y4,i)[1],lerp(x3,y3,x4,y4,i)[2],i)[1] local yb2 = lerp(lerp(x2,y2,x3,y3,i)[1],lerp(x2,y2,x3,y3,i)[2],lerp(x3,y3,x4,y4,i)[1],lerp(x3,y3,x4,y4,i)[2],i)[2] local x = lerp(xb1, yb1, xb2, yb2, i)[1] local y = lerp(xb1, yb1, xb2, yb2, i)[2] line(xlast, ylast, x, y,2) xlast, ylast = x, y end end
function TIC() cls() -- Set x,y of mouse _,_, mouseOn = mouse() if mouseOn then x,y = mouse() print(x..":"..y,x+20,y) end
-- Drawn a quadratic bezier if mode == 0 then bezierQuad(0, 60, x, y, 240, 60) -- Show point if mouseOn then circ(x,y,2,3) else print("Quadratic Bezier",10,120,13) end end -- Drawn a cubic bezier if mode == 1 then bezierCub(0, 60, x/2, y, 120+x/2, 135-y, 240, 60) -- Show points if mouseOn then circ(x/2, y,2,3) circ(120+x/2, 135-y,2,3) else print("Cubic Bezier",10,120,13) end end if btn(4) then mode = 0 elseif btn(5) then mode = 1 end end
| Status | Prototype |
| Category | Other |
| Platforms | HTML5 |
| Author | Jiant Studios |
| Genre | Educational |
| Made with | TIC-80 |
| Tags | bezier, Dark, Math, Prototype, sourcecode |
Download
Download NowName your own price
Click download now to get access to the following files:
cart.tic 3.4 kB
Comments
Log in with itch.io to leave a comment.